いきなりですが、合同って覚えていますか?
二つの三角形があって、辺の長さとか角度が与えられるので、それらを使って確かに同じ三角形であることを証明するみたいな問題です。
覚えていないですけど、合同という言葉は小学校5年生で習うみたいです。その時は証明じゃなくて、与えられた三角形と同じ三角形を定規やコンパスで描くという問題のようです。
似たようなもので、相似というのもありましたね。
形は同じだけど、大きさが違う三角形などです。

で、この合同や相似の何が重要かというと
続きを読むいきなりですが、合同って覚えていますか?
二つの三角形があって、辺の長さとか角度が与えられるので、それらを使って確かに同じ三角形であることを証明するみたいな問題です。
覚えていないですけど、合同という言葉は小学校5年生で習うみたいです。その時は証明じゃなくて、与えられた三角形と同じ三角形を定規やコンパスで描くという問題のようです。
似たようなもので、相似というのもありましたね。
形は同じだけど、大きさが違う三角形などです。

で、この合同や相似の何が重要かというと
続きを読む最近働き方や収入が変わったこともあり、加入している生命保険を見直す機会がありました。
今入っている保険は社会人に入って1年目で加入したので、正直全くお金の知識もなく、ほとんど言われるがままの保険に加入したのですが、今回は保険の意味から見つめ直して選んでみようと思いました。
ここ2週間ほどは生命保険数理や金融工学の本を読んでみたり、
数式や計算結果と睨めっこしていました。
一応(31歳時点の)僕なりの結論みたいなのが出たので、こういう風に考える人もいるんだな程度で読んでほしいです。
結論部分は「保険の考え方」セクションに書いてあるので、「保険の期待値」は飛ばしてもらって大丈夫です。
結果だけ先に書いておくと
ところで、100円のりんごと50円のりんごだとどちらが得でしょうか?
あるいは、2mの紐と4mの紐ではどちらが長いでしょうか?
物の価値や基準が定まっていると、比較することは容易な場合がほとんどです。
しかし、保険の場合は起こるか起こらないかわからないモノに対して値段がついているから、保険の商品が商品が得かどうかなんて言うのは簡単ではありません。価値が確率的に変化してしまうからです。
価値が確率的に変化してしまうもの同士を比較する場合の一つの方法が期待値を計算することです。
期待値は確率的に複数の価値が発生する物をたった一つの数値に変換する技法です。意味としては平均と同じです。
比較することにはよく使われる指標ですが、個別の情報を握りつぶしていると言う点だけは注意が必要です。
保険の商品と一口に言っても色々あるので、ここでは以下のような保険を考えて、保険に加入した場合と加入しなかった場合の期待値を求めてみたいと思います。ただし詳細は省きます。
「保険金は入院時に一度だけ支払われて、支払う回数に制限はないものとする。この保険は定期保険で、入院する確率は年齢によって変化しない 」
計算のために、変数を決めておきます。
支払われる金額をH円、毎月の保険料をh円、保険期間(月)をnカ月, 入院時にかかるお金をN円、人生の中でたった一回だけ入院する確率をp
そうすると、期待値はこんな感じになります

言い換えると
保険加入時の期待値は、「保険金の期待値 - 入院費の期待値 - 総支払額」
一方で非加入時はただ損失があるだけなので「-入院費の期待値」
となります。
で、どっちがお得なのよ?を調べるために引き算します。

これがマイナスになるときは保険に入ると損で、プラスになると入った方がお得ということになります。
よくみてみると、支払われる保険金の期待値と、支払う保険料の対決みたいな構図になっていますね。
とりあえず、プラスになる方に賭けてみましょう。
ちょちょっと式変形をして
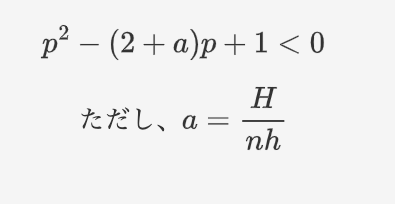
懐かしい!二次方程式が出てきました!
pは0より大きいので、上に広がっている正統派の二次関数です。
この関数が0より小さくなるのは、下の図で言うと赤い線のところです。数値は適当です。
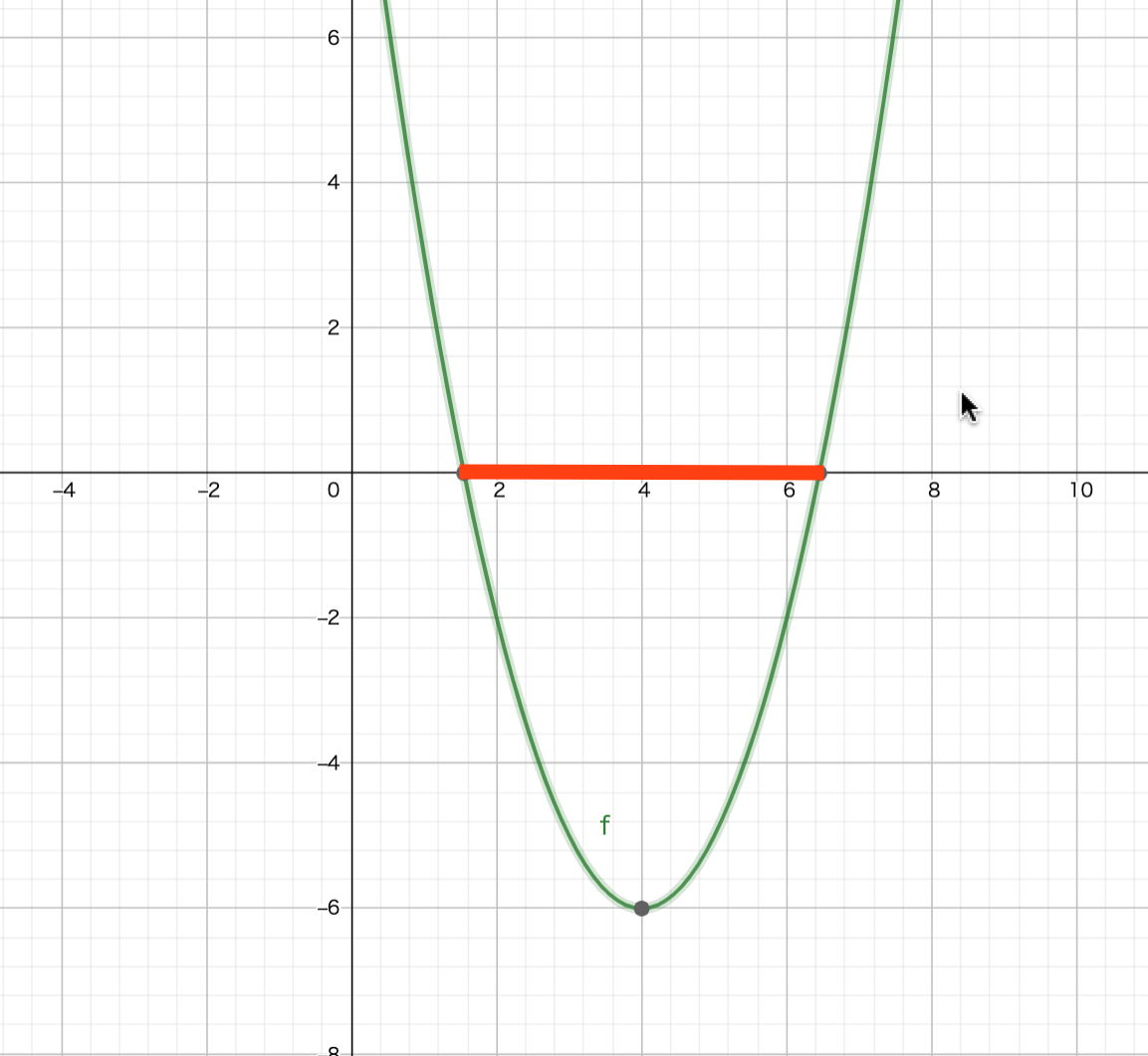
二次関数が出てきたので、素直に解の公式を使ってx軸と交わるところを探しましょう。
そうすると、
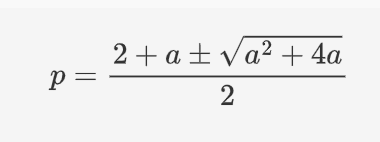
こんな感じで求まります。
プラスの方は「1+(その他 > 0)」の形になり、pが1以下であることと反するので今回の答えではありません。
一方マイナスの方は
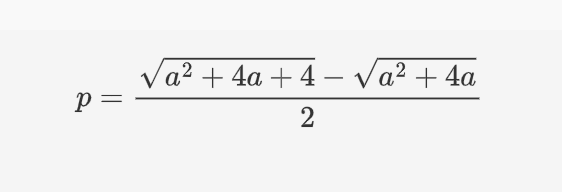
のように変形できます。見ての通り分子は必ず正の値を取り、しかもうまいこと1より小さくなります。確率の値としては合格ですね。
つまり、保険に入った方がお得になるような確率pは

こんな範囲の中のものに限ると言うことです。
ある一定以上の確率で発生しないと入るだけ損ということですね。
左側の式は保険金と保険料の比率であるaの関数になっています。これをグラフで表すと

こんな感じになります。
例えば、x軸が1のところを見ると、大体0.4つまり40%です。
これが意味するところは、「保険金と保険料がほぼ一緒の保険があったときには、保険金が支払われる確率(入院とか)が40%を超えていたら加入した方が期待値が高い」となります。
0.5は保険金が保険料の半分になっていますね。こんなの損じゃないかと思うかもしれませんが、確率0.5だったら一生のうちに2回か3回は発生する確率も高いので、こんな感じになっています。
保険料に対して保険金が10倍とかの保険になってくると、グラフの値も低くなってきます。つまり得になるハードルが下がるイメージです。
先ほどの計算は計算してみた保険商品の一つです。色々なパターンが考えられるので、同様の流れで計算したものと、実際にこのグラフと実際に提案してもらった保険商品とを比較してみたのですが、期待値的には加入した方がかなり損になることがわかりました。
これは考えてみれば当たり前で、期待値で考えてみれば、保険屋さんに入るお金と出るお金が差し引き0でようやく損得なしの状態なんですね。
けど保険屋さんのテナント代や役員報酬、準備金、従業員の給与など保険金以外にでていくお金はたくさんあります。
つまり入ってくるお金よりも保険金としてでていくお金はだいぶ低いです。パチンコと同じですね。
じゃあ僕は保険に入らない決断をしたのかというと全くそんなことはないです。
さて、ここまでは長い前置きでした。
期待値は先ほども書きましたが、確率的に変化する価値を比較するときには便利なのですが、個別の情報を握りつぶしてしまう特性があります。
何を握りつぶしているのかというと、実際に入院を行った人の貯金額の変動ですね。
保険に入らずに入院したために貯金がマイナスになってしまったり、あるいはそんなこともなかったり。色々なパターンが考えられますが、これらを無理やり一つの値にしたのが期待値です。
考えなければならないのは、期待値ではなくて、リスクの大きさです。
確率がいくら低くても、発生するときは発生します。そのときそのリスクを許容 できない場合は悲惨な結果が待っているでしょう。
許容できるとは、リカバリーできるかどうかみたいなイメージです。例えば高度障害で働けなくなり、給料も減ってしまい、貯金が底をついて子供を大学や高校に行かせられないとかですね。
逆に許容できるパターンとしては、数日の入院で15万円支払い、収入も20万減った場合ですが、これは貯金が100万円あればマイナスになることもなく、また働けば貯金は増えてきます。
許容できないリスクに対しても保険をかけておけばプラスになるやん!という考え方もありますが、保険に加入した時点で保険料を支払わなくてはなりません。
保険料の支払いは確率100%で発生する損失です。
入院を満期までしなければただ単純に保険料分だけ損をします。保険に入っていなければ損はなかったことになります。
また、保険商品の中には終身の死亡保険もあります。これは確率100%で保険金が支払われますし、保険会社で運用していけば払った額よりも多く返ってくるものもあります。
これを期待値だけで考えると入った方が得という結論になってしまうのですが、終身保険というのはその分保険料が高いです。
そして保険金を受け取るのは寿命でなくなるとすると90や100歳になってからでしょうう。
その場合、支払った保険料というのは死ぬまで手をつけられないお金になります。
死んだ後にお金を残せるが、保険料を支払ったため貯蓄が少なく老後が貧しいというのは本末転倒でしょう。
万が一があった時のためにも、ランニングコストは極力下げるべきです。

長くなってしまいましたが、、、
まとめると、保険は基本的に加入しないという前提で、許容できないリスクに対しては保険で備えておく。支払う保険料もリスクになるので欲しい金額ではなくてリカバリー可能な最低ラインで考える。
というのが僕の出した結論でした。
タイトルの通りです。2年前の今日、育児休業が始まりました。 子供に怒ったことも、妻と喧嘩したこともありました。怖いマンションのオーナーと真下の階の住人に悩まされたりもしましたが、ほとんど毎日爆笑しながら過ごした2年間でした。
これから育児休業を取ろうと思っている人、育児に積極的に参加しようとしている方に向けた文章を書きたいのですが、正直何を書けばいいか分からないので、育児休業取ったある男性が、この2年間で何を思ったのか、残しておこうと思います。
比較的最近出版されている習慣や学習の本を見てみると、脳科学のデータや論文を引用し応用することが主流になってきているように思える。
脳科学というと心理学と似たような学問のように考えてしまうが、興味を持って最近出版された脳科学の本を何冊か読んでみると、全く別の考え方に根差した学問であることが分かった。
脳科学と心理学の大きな違いは、脳科学が脳の内部反応を見ているのに対し、心理学は外部反応を見ている。
脳科学では外からの刺激に対し、脳のどの部位が反応して、結果どのようなホルモンが出たり、体にどのような反応がでるのか調査する。調査した結果、異なる外部刺激であっても、同じ部位が反応すれば、同じような反応をしていまうということも分かっている。 その最も顕著な例が「共感」である。誰かがひどい目にあわされたり、ホラー映画で痛々しい場面があると、「胸が痛む」「同じ場所がムズムズする」といった反応が起きるが、この時、実際にケガをした場合に反応する脳部位と同じ場所が強く反応する。つまり「本当に」痛みを感じている。
一方、心理学はアドラーのような個人の心理学を除けば、統計学とほぼ等しい。ある集団に対して、外部刺激を与え、その刺激に対してどのように反応するかのデータを取る。例えば、学生が教室で告白するのと、つり橋の上で告白するのとでは、カップルが成立する確率に明確な差があるのかどうかを検証する。統計的に有意な差があれば、それは心理学的に効果があると認められる。
心理学は統計的に有意が判定できるだけのデータが集まれば効果を検証することは容易いが、脳科学の調査は脳波や電気信号、活動領域を調べないといけないため、心理学よりも調査が難しい。きわめて医学的な分野となる。
最近になって、ようやく脳活動の詳しいメカニズムが解明されてきた。いくつかの本のまとめにすぎないが、ここでは脳について分かっていることを、家でできる実験を交えて紹介したいと思う。
前半は脳について分かっている基本的な事柄を書き、後半は実験を交えて驚くべき脳の機能を見ていく。
続きを読む2016年ごろからITエンジニア業界では(第3次)AIブームが起こりました。第3次と書いたのは、実はブームになるのはこれで3回目です。
その後、数年かけて実験・開発が繰り返され、2018年ごろから様々なAI関連商品やサービスが誕生しました。
みなさんのAIに対するイメージってどんなものでしょう?
テレビではよく「〇〇を学習して××なAIが誕生した」みたいに言われています。
が、コンピュータが学習ってどういうこと?って思いませんか。
そこで今回はざっくりと現在作られているAIについて解説し、AIが得意なこと、苦手なことなどを書いてみようと思います。
【目次】
続きを読む
プログラミングスクールの講師をやっている中で、基本的な構文は分かったけど、いざプログラムを書くとなったら何をしていいかわからない。手が動かない。と言う方がほとんどです。
そこで今回は、まずそもそもプログラミングって何?という話をします。話の中でプログラミングとプログラムという言葉が出てきますが、プログラム(文字)を考えて入力する行為がプログラミングになります。混同しないように注意して下さい。
プログラミング(またはプログラム)が何か説明した上で、プログラムを書く方法をお伝えします。ただし、具体的なプログラミングの書き方やコードの説明ではありません。
最終的にアルゴリズム≒プログラムという結果になるので、タイトルは「アルゴリズムってなんだろう?」にしています。
また、小学校からプログラミング教育(いわゆるプログラミングじゃなくて、プログラミング的な考え方、要するにアルゴリズム)が始まるそうです。もう始まっているのかな。この文章はプログラミングを教えることになったけど、今いちよく分からんという講師・教師に向けたものでもあります。
一プログラマの意見ですが、参考になれば幸いです。
【目次】
続きを読む
自分の子供や親せきのお子さんの誕生日やクリスマスにプレゼントするものって迷いますよね。クリスマスはお子さんが欲しがってるものでしょうか。
誕生日は年齢も上がるし、お兄ちゃんお姉ちゃんになっていくので、おもちゃ以外のものを送りたい。そう考えている方も多いはず。
私は迷わず図鑑をお勧めします!
なぜプレゼントに図鑑をおススメするかと言うと、
続きを読む