Qiita Processing Advent Calendar 2018　12月12日に投稿した記事です

はじめに

scaleやtranlateは書く順番によって結果が異なるって知ってましたか？

本記事は、transform系関数(scale,translate,rotate)を行列で表現し、深く理解することで正しく使えるようになるための講座です。

どのようなときに結果が異なるのか・一致するのか、なぜそのようなことが起こるのか、ベクトルと行列を使ってその謎に迫っていきます。

内容は数学ですが、ベクトルや行列に関する前提知識は必要ありません。ベクトルとは何かから始めていきます。

なぜ行列なのか

Processing(p5js)では線分の開始・終了位置や、円の中心、四角形の四隅など、あらゆる点がx-y座標で表現されています。

座標上の点というのは、言い換えれば原点を始点としたベクトルが指し示す点です。

あるいは、ボールが壁にバウンドするようなアニメーションを考えるときでも、ボールの速度はベクトルで表現されます。

そう、Processingはベクトルで支配されているといっても過言ではないのです。

そんなベクトルを簡単に操作できるツールが行列なのです。

実際、ProcessingにはapplyMatrixという行列を座標全体に作用させる関数が存在します。

そして、scaleやtranslate,rotateなどのtransform系関数はすべてapplyMatrix関数一つで代用が可能なのです。

本記事には華々しいProcessing作品やコードは出てきませんが、Processingの理解はぐっと深まるはずです！

最初は少し退屈かもしれませんが、最後までお付き合いください。

【目次】

はじめに
なぜ行列なのか
ベクトルとは
ベクトルの演算
行列
行列の合成
- 行列同士の掛け算
- 同じ種類の行列であれば可換になる
回転
- rotate関数
- その場で回転させたいんだ！
まとめ
最後に
おまけ

ベクトルとは

さて、改めてベクトルとは何でしょうか。

最も簡単な言葉で言えば、「数字のペア」となります。

原点から見て、x座標(右方向)にどれくらいか、y座標(下方向)にどれくらいかを（）を使って $(10, 29)$ と書いたりします。

もう少し難しい言葉で言うと、「定数倍と足し算が定義されているものの集まり」をベクトル空間と呼び、ベクトル空間の一つ一つの要素のことをベクトルと呼びます。

定数倍(ある数をかける)してもベクトルはベクトルのまま

$10 × (10, 20) = (100, 200)$

足し算してもベクトルはベクトルのまま

$(50, 50) + (10, 20) = (60, 70)$

普通の数字であれば引き算や割り算もできますが、ベクトルはこの二つの演算しかできません。

「引き算はできないの？」

A.次のように、引き算も定数倍と足し算で可能です

$(10, 20) - (5, 5) = (10, 20) + (-1) × (5, 5) = (5 ,15)$

ベクトルの基本的な概念は以上です。とてもシンプルですが、これでProcessingが支配されているのです。

では次からはもう少しProcessing寄りの話をしましょう。

ベクトルの演算

改めて和と定数倍を見ていきます。

和

ベクトルを昔懐かし矢印で描いてみます。矢印の開始地点を「始点」、矢印の終了地点を「終点」と呼びます。

ベクトル

二つのベクトルがあった時に、ベクトルの和とは何を指すのでしょうか

それは、ベクトルをつないで、始点と終点を結んだ「新しいベクトル」です。

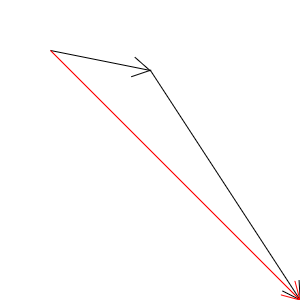
ベクトルとは、横方向にどれくらい、下方向にどれくらいという量であって、原点から見てどの場所というような絶対的な位置を表すものではないことに注意しましょう。

なので、ベクトルの足し算を行うときは、後ろのベクトルは前のベクトルにつながれるのです。

ベクトルの和が良く表れるのはtranslate関数を使ったときでしょう。

translate関数は指定したベクトルの分だけ座標全体を移動する関数です。

簡単に言えば、画面中央に描かれる円があった時に、translate(100, 100)とすれば円はxy方向にそれぞれ100ずつずれます。

ellipse(100,100,100);

translate(100,100);
stroke("red");
ellipse(100,100,100);

translateのサンプル

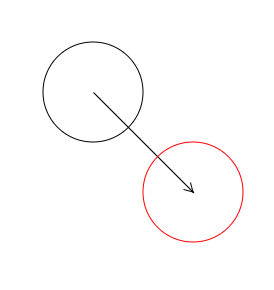
実はこれこそまさに「ベクトルの和」なのです。

$(100,100)$ という座標は、translateで指定したベクトルを足すことで、translate後の表示位置を知ることができます。

$$ (100,100) + (100,100) = (200,200) $$

translate関数は続けて呼び出すことで、効果が重ね掛けされます。

translate(100, 100);
translate(-100, 100);

translateのサンプル2

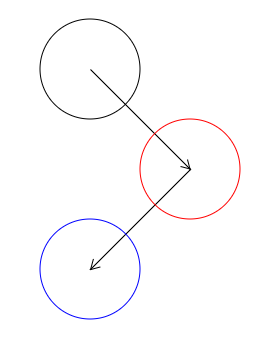
重ね掛けされたtranslateはベクトルの和を使って一つのtranslateにまとめることができます

$(100, 100) + (-100, 100) = (0, 200)$

//translate(100, 100);
//translate(-100, 100);
translate(0, 200)

普段からtranslateを使っている方であれば、わざわざベクトルを意識しなくても、頭の中で計算しているかもしれません。

こんな感じで次もベクトルの演算とProcessingでの関数との対応を見ていきます。

定数倍

次は定数倍です。これはscale関数によって実装されています。

scaleは指定した定数を座標全体にかける関数です。

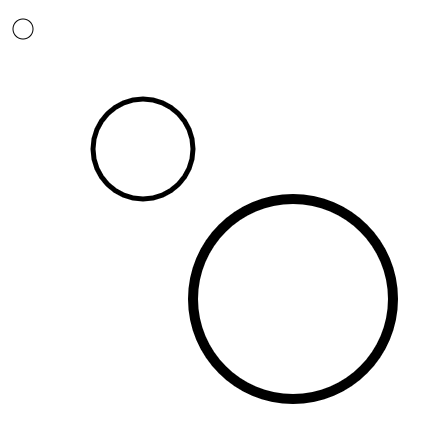
簡単に言えば、 $(30,30)$ に描画される円があった時にscale(5)とすれば、円は $(150, 150)$ の位置に描かれます。

ellipse(30, 30, 20);
scale(5);
ellipse(30, 30, 20);

scaleサンプル

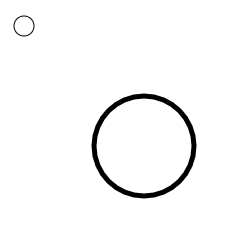
ただし、見ての通り、座標全体が拡大されているので、半径や線の太さも5倍になります。

$5 × (30, 30) = (150, 150)$

scale関数も複数回呼び出すと、効果が重ね掛けされます。

ellipse(30, 30, 20);
scale(5);
ellipse(30, 30, 20);
scale(2);
ellipse(30, 30, 20);

$5 × 2 × (10, 10) = 10 × (10, 10) = (100, 100)$

scaleサンプル2

三角形の内部を表現する

定数倍と和を応用した例を見てみましょう

今、二つベクトルがあるとします。 $(100, 20), (50, 200)$ 。このベクトルをそれぞれa, bと呼ぶことにします。

原点を始点として、点(100, 20)を指し示すベクトルはaです。

点(50, 200)を指し示すベクトルはbです。

少々天下り的(最初から答えが分かっているかのような論法)ですが、aとbはそれぞれこんな風にも書けます

$$ (100, 20) = 1×a + 0 × b = a\\ (50, 200) = 0×a + 1 × b = b $$

aのベクトルは1を1と0に分解し、bのベクトルは1を0と1に分解していると見ることができます。

それでは、1を0.5と0.5に分解すると、どのようなベクトルになるでしょうか

$$ 0.5× a + 0.5 × b = (50, 10) + (25, 100) = (75, 110) $$

図に書くとこんな感じです

三角形の内分

では、半々ではなくて、0.7と0.3, 0.1と0.9のように1を分解したベクトルはどうなるでしょうか

三角形の内分２

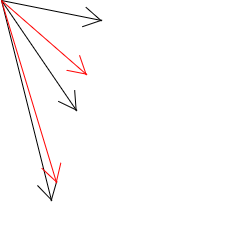
じつは、

$$ c = r × a + s × b　（r , s は足すと1になるようにする) $$

で表されるベクトルcが指し示す点の集合(点を集めると線になる)は、二つのベクトルで作られる3角形のもう一つの辺となるのです。

三角形の内分4

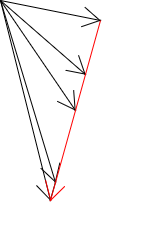
では、足し合わせて1というルールを少し変えて、足し合わせた数が1以下になるようにしてみます。

$$ c = r × a + s × b　（r + s が1以下になるようにする) $$

このとき、rとsをいろいろ変えて作ったベクトルcが指し示す点を集めると、三角形の内部となるのです

原点から、これらのベクトルが指し示す点まで線分をいくつか描くとこんな感じになります。

三角形の内分3

r+sの値によって色を分けてあります。

内積

続いては、内積を見てみましょう。内積はベクトル同士の掛け算です。

内積の値自体はあまりProcessingで使わないのですが、その計算方法はこの後の行列での計算で使うので、どうやって計算されるのか見ていってください。

いま、ベクトルが2つあるとします。 $(100, 200), (10, 80)$

このベクトルの内積は、次のように計算します。

$$ (100, 200) \cdot (10, 80) = 100×10 + 200×80 = 1000 + 16000 = 17000 $$

ベクトルの内積は、それぞれ1番目の値同士、2番目の値同士をかけ合わせて足し算します。内積の計算結果は一つの値となります。

本来のベクトルの教科書であれば、内積について言うべき重要な性質がたくさんあるのですが、Processingで内積はあまり使わないので、これ以上は書かないことにします。

行列

ベクトル自体の説明はこれくらいにして、行列について説明したいと思います。

行列とは

行列は、縦横に数字が並んだものです。

$$ \begin{pmatrix} 3 & 4 \\ 1 & 3 \end{pmatrix} $$

行列はサイズ（縦横の大きさ）が重要で、2行2列(縦に2行、横に2列)を2×2行列と言ったり、

2行3列の行列を2×3行列と言ったりします。読み方は「にかけるさんぎょうれつ」です

2×3行列の例

$$ \begin{pmatrix} 3 & 4 & 5\\ 1 & 3 & -1 \end{pmatrix} $$

2次元ベクトルの世界では、2×2行列が特に重要です。ただしProcessingで行列を扱うときは内部で3次元ベクトルとして扱っているので、コードを書くときは3×3行列を扱います。詳しくは後述します。

また、行列に名前を付けるときは慣例的に大文字のアルファベットを使います。AとかBとか

行列はこれだけ眺めていてもあまり楽しくないのですが、ベクトルに作用させるととても楽しくなります。

行列の作用

では、行列をベクトルに作用させてみたいと思います。

これまでベクトルは横方向に書いていました $(1,2)$ 。ですが、掛け算の右側にいるときは、ベクトルは縦方向に書きます。

$$ Aa = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} $$

普通の掛け算と違い複雑ですが、作用させた結果は次のようになります。

$$ Aa = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax + by \\ cx + dy \end{pmatrix} $$

行列の1行目をベクトルと見たときに(今だと $(a , b)$ )、ちょうど、行列の1行目のベクトルと、ベクトル $(x ,y)$ の内積が、新しいベクトルの1行目の値となります。

同じように、行列の2行目のベクトル $(c, d)$ と、ベクトル $(x, y)$ の内積の値が、新しいベクトルの2行目の値となります。

このように、行列をベクトルに作用させると新しいベクトルになるのです。

具体例を見てみましょう

$$ A = \begin{pmatrix} 1 & 2\\ 3 & 4 \end{pmatrix}, a = (50, 60) $$ 行列Aとベクトルaの掛け算（行列の作用）は次のように計算します。 $$ Aa = \begin{pmatrix} 1 & 2\\ 3 & 4 \end{pmatrix} \begin{pmatrix} 50\\ 60 \end{pmatrix} = \begin{pmatrix} 1 * 50+ 2 * 60\\ 3 * 50 + 4 * 60 \end{pmatrix} = \begin{pmatrix} 170\\ 390 \end{pmatrix} $$

となります。

行列を四角形の四隅の座標に作用させることで、4角形がどのように変化するのか見てみましょう。

matrixサンプル

行列が適当なのであまり面白い例ではなかったですね。もう少ししたらちゃんと意味のある行列を扱います。

毎回手で行列の計算をプログラミングしていくのは大変ですね。

大丈夫です。Processingには座標全体に行列を作用させる関数がちゃんと用意されています。

こちらはあまり使ったことが無いかもしれません。applyMatrixという関数です。

matrixは行列で、applyは適用という意味です。

applyMatrixが座標全体に作用させる行列は、次のような3×3行列です。

$$ \begin{pmatrix} a & c & e\\ b & d & f\\ 0 & 0 & 1 \end{pmatrix} $$

2次元なのに、3×3行列なのは不思議に思うかもしれませんが、e,fは平行移動を表現するために必要なのです。

プログラム上では $(x, y)$ の2次元ベクトルを扱うのですが、内部では行列に作用させるベクトルは $(x, y, 1)$ のようになります。

2次元ベクトルを一時的に3次元に拡大することで、ベクトルの作用の幅を広げる数学的なテクニックです。

さて、applyMatrixの使い方はこんな感じです。プログラム中のa,b,c,d,e,fは上に書いてある行列と対応しています。

//applyMatrix(a,b,c,d,e,f);
quad(10,10,60,11,50,41,15,38);
applyMatrix(1,3,2,4, 0, 0);
stroke("red");
quad(10,10,60,11,50,41,15,38);

この結果は上の行列を作用させた四角形の図になります。

translateもscaleもapplyMatrixで書ける

これまでtranslateやscale,applyMatrixと座標を変形させる関数を紹介してきましたが、実は、translate(移動)もscale(定数倍)もapplyMatrix一つで対応できてしまうのです。

translate

次の2つは同等なコードです

translate(10, 50);
point(10,10);

applyMatrix(1,0,0,1,10,50);
point(10,10);

ベクトルと行列で考えてみましょう

まず、translateはベクトルの足し算でした、

$$ (10, 10) + (10, 50) = (20, 60) $$

applyMatrixは次のように計算されます。

$$ \begin{pmatrix} 1 & 0 & 10\\ 0 & 1 & 50\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 10\\ 10\\ 1 \end{pmatrix}= \begin{pmatrix} 10×1 + 10×0 + 1×10\\ 10×0 + 10×1 + 1×50\\ 10×0 + 10×0 + 1×1 \end{pmatrix}= \begin{pmatrix} 20\\ 60\\ 1 \end{pmatrix} $$

最後に1がついていますが、x,y座標の値は確かに同じになりました。

より一般的に書くと、translateと同等なapplyMatrixは次のようになります。

translate(a,b);

applyMatrix(1,0,0,1,a,b);

ベクトルと行列を3次元に拡張したおかげで、移動も行列の作用として表現することができるのです。

scale

scaleはtranslateよりもう少し簡単です。次の二つのコードは同じ結果になります。

scale(10);
point(10, 10);

applyMatrix(10,0,0,10,0,0);
point(10,10)

こちらもベクトルと行列で計算します。

まずscaleは単なる定数倍でした。具体的な数ではなく、何か任意の定数をcとしておきます。

$$ c×(10, 20) = (10c, 20c) $$

これに対応する行列は次のようになります。

$$ \begin{pmatrix} c & 0 & 0\\ 0 & c & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 10\\ 20\\ 1 \end{pmatrix}= \begin{pmatrix} 10c\\ 20c\\ 1 \end{pmatrix} $$

こちらも、同じ結果になるのが分かるかと思います。

行列の連続作用

それでは、次のような、「scaleしてからtranslate」というコードは行列を用いると、どう表現されるでしょうか。

scale(2);
translate(30, 50);
ellipse(100,100,100);

このコードをベクトルと行列で計算してみましょう

コード上ではscaleの次にtranslateが適用されているように見えますが、実はProcessingでは後から書いた方が先に適用されるのです。

なので、まずはtranslateを表現する行列から作用させていきます。

$$ \begin{pmatrix} 1 & 0 & 30\\ 0 & 1 & 50\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 100\\ 100\\ 1 \end{pmatrix}= \begin{pmatrix} 130\\ 150\\ 1 \end{pmatrix} $$

次に、この $(130, 150, 1)$ をscaleします。

$$ \begin{pmatrix} 2 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 130\\ 150\\ 1 \end{pmatrix}= \begin{pmatrix} 260\\ 300\\ 1 \end{pmatrix} $$

この計算が正しいことを実際にProcessingで書いて実験してみましょう

    ellipse(100,100,100);//元の円

    // scaleとtranslateを適用
    push();
    stroke("red");
    rectMode(CENTER);
    scale(2);
    translate(30, 50);
    ellipse(100,100,100);
    pop();

    ellipse(260, 300, 10);//行列の作用を計算した値

f:id:s-uotani-zetakansu:20181206095729p:plain — 左上：元の位置、赤円：移動後の位置、小さい円：行列によって計算した移動後の位置

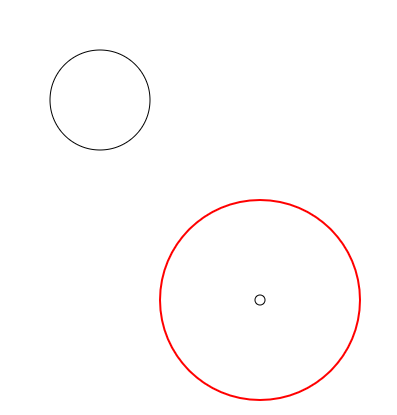
左上の円が何も作用させていないときの円、赤い円がscale,translateを作用させたときの円です。

赤い円の中央にある小さい円が、行列によって計算した座標位置を表しています。赤い円と小さい円の中心座標が同一であることが分かります。

さて、translateやscale関数の適用は、行列の演算に直せるということを理解できたかと思います。

それでは、「行列を2回連続で適用させること」と、2つの行列をあらかじめ合成しておいて「合成してできた新しい行列を適用させること」が同等であるということを次で見ていきます。

そして、Processingでscaleやtranslateを使う上で注意すべき衝撃の真実をお伝えしたいと思います。

勘のいい方はもうお分かりかと思いますが、行列は積に関して非可換です。

行列の合成

行列の合成は行列や計算がたくさん出てきて目が疲れるので、綺麗な画像をみて少し休憩しましょう。

f:id:s-uotani-zetakansu:20181206100748j:plain — 頭がスッキリしそうな綺麗な夕日の写真

行列同士の掛け算

行列は行列同士掛け算することができます。ベクトル同士の掛け算(内積)はある数値を出力するのに対して、行列の掛け算は新たな行列を生み出します。

行列の掛け算のルールはかなり特殊です。

$$ \begin{pmatrix} 1 & 2 \\ -2 & 1 \end{pmatrix} × \begin{pmatrix} 1 & 3 \\ 2 & 5 \end{pmatrix} $$

この掛け算を例にとって説明します。

この行列の積の結果は2×2行列になるのですが、まずは左上の値を計算していきます。?の位置の値です。

$$ \begin{pmatrix} ? & *\\ * & * \end{pmatrix} $$

まず、1つ目の行列の1行目を抜き出します。

$$ \begin{pmatrix} 1 & 2 \\ -2 & 1 \end{pmatrix} -> (1, 2) $$

次に、2つ目の行列の1列目を抜き出します。

$$ \begin{pmatrix} 1 & 3 \\ 2 & 5 \end{pmatrix}-> \begin{pmatrix} 1\\ 2 \end{pmatrix} $$

抜き出した2つのベクトルの内積を計算します。

$$ (1, 2)\cdot(1, 2)=1×1 + 2×2 = 5 $$

この値が新しい行列の1行目の1つめの値となるのです。

$$ \begin{pmatrix} 5 & *\\ * & * \end{pmatrix} $$

同じような計算で、

1行目の2番目＝ 1つ目の行列の1行目　× 2つ目の行列の 2列目
2行目の1番目＝ 1つ目の行列の2行目　× 2つ目の行列の 1列目
2行目の2番目＝ 1つ目の行列の2行目　× 2つ目の行列の 2列目

日本語で書いてもややこしいので、ここは数式の力を借ります。

行列の要素を表すのに $a_{ij}$ という記号を導入しましょう。

iは行番号、jは列番号を表していて、この記法で行列を書くと次のようになります。

$$ \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} $$

[tex a_{21}]は2行目の1列目を表します。

この記法を使うと行列の掛け算はこんな風に書けます

$$ A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} $$

のとき、

$$ AB = \begin{pmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \end{pmatrix} $$

Aの横×Bの縦と覚えてください。

さて、行列の積の方法が分かったところで本題です。

行列の積には結合法則が成り立ちます。すなわち、A,Bを行列、aをベクトルとして、

$$ (A × B)a = A(Ba) $$

が成り立つのです。

右辺の $A(Ba)$ というのは、Bを先に作用させて、そのあとにAを作用させるという意味になります。

左辺の $(A × B)a$ は、AとBを先に掛け算しておいて、その結果の行列をaに作用させるという意味です。

この意味で、行列どうしの掛け算は合成と呼んでいます。

先ほど「scaleしてからtranslate」がどうなるのか計算しました。その時の計算方法は右辺の $A(Ba)$ と同じく、連続して作用させるものでした。

ここでは、先に行列を合成しておいて、あとからベクトルに作用させる方法で再度計算してみます。

scale,translateはそれぞれ次のような行列で表現されるのでした。便宜上、それぞれ $S, T$ と名前をつけます。

$$ scale -> S= \begin{pmatrix} c & 0 & 0\\ 0 & c & 0\\ 0 & 0 & 1 \end{pmatrix}, translate -> T= \begin{pmatrix} 1 & 0 & a\\ 0 & 1 & b\\ 0 & 0 & 1\\ \end{pmatrix} $$

さらに、scaleを書いたあとでtranslateを書くと、先に適用されるのはtranslateでした。途中経過は大変なので書きませんが、次のようになります。

$$ S(Tx) = (ST)x = \\ \begin{pmatrix} c & 0 & 0\\ 0 & c & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & a\\ 0 & 1 & b\\ 0 & 0 & 1\\ \end{pmatrix}x = \begin{pmatrix} c & 0 & ac\\ 0 & c & bc\\ 0 & 0 & 1\\ \end{pmatrix}x $$

では、上で出てきた例

sclae(2); //c=2
translate(30, 50);//a=30, b = 50
point(100,100);

を当てはめて計算してみます。 $(260, 300)$ になるはずです。

$$ (ST)x = \begin{pmatrix} 2 & 0 & 60\\ 0 & 2 & 100\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 100\\ 100\\ 1 \end{pmatrix}= \begin{pmatrix} 2×100 + 0×100 + 60×1\\ 0×100 + 2×100 + 100×1\\ 0×100 + 0×100 + 1×1 \end{pmatrix}= \begin{pmatrix} 260\\ 300\\ 1 \end{pmatrix} $$

ということで、無事行列の連続作用は合成してから作用することで表現できました。

しかし、ここで本当に言いたいことは、行列の結合法則ではありません。もっと重要なことです。

実は、行列の積は可換ではありません。すなわち、 $A×B$ と $B×A$ は等しいとは限らないのです。！

つまりどういうことでしょうか。

$AB \neq BA$ すなわち、 $A(Bx) \neq B(Ax)$ ということ、要するに、「scaleのあとにtranslate」と「translateのあとにscale」は異なる結果になかもしれないということです。（積の順番を入れ替えても等しくなる場合もあります。）

実際、先ほどとは逆順の $TS$ を計算してみます。

$$ TS = \begin{pmatrix} 1 & 0 & a\\ 0 & 1 & b\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} c & 0 & 0\\ 0 & c & 0\\ 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} c & 0 & a\\ 0 & c & b\\ 0 & 0 & 1 \end{pmatrix} $$

たしかに、 $TS$ は $ST$ と異なる行列になりました。

プログラムでも確かめてみましょう。

    push();
    stroke("blue");
    scale(2);
    translate(100,100);
    ellipse(0,0,50);
    pop();

    push();
    stroke("red");
    translate(100,100);
    scale(2);
    ellipse(0,0,50);
    pop();

f:id:s-uotani-zetakansu:20181206103221p:plain — 青：scale->translate, 赤：translate->scale

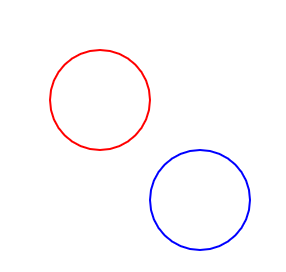
円が別々の位置に表示されているのが分かります。

これまで、私も何度も記述する順番で結果が異なることに悩んでいました。

なんとなく経験的に後に記述した方が先に適応されると感じていたのですが、行列として表現し、実際に掛け算してみると結果が異なるということを確かめられてこれまでのモヤモヤがすっきりしました。

適用の順番に関しては、「scaleの後にtranslate」を記述した場合だと、 $ST$ を適用したことになるので、書いた順番に行列が並べられてベクトルに作用していくと覚えるといいでしょう。

同じ種類の行列であれば可換になる

$S$ や $T$ など、異なる動きをする行列は非可換(作用させる順番、すなわち積の順番を入れ替えると結果が異なる)でした。

しかし、同じ種類であれば可換となります。今、 $c, d$ 倍するscaleの行列を $S(c), S(d)$ と表すと、

$$ S(c)S(d) = S(d)S(c) = S(c×d) $$

が成り立ちます。意味を考えてみると、2倍してから5倍するのと、5倍してから2倍するのとでは、当然結果は同じ10倍になります。

translateを表す行列Tでも同じです。 $(a,b),(e,f)$ だけ移動する行列を $T(a,b), T(e,f)$ とすると、

$$ T(a,b)T(e,f) = T(e,f)T(a,b) = T(a+e, b+f) $$

これらは実際に行列の積を計算すればすぐわかるので、ぜひ証明に挑戦してみてください。

移動でも定数倍でも、次に紹介する回転でも、行列で表現すると作用の合成がすべて行列の積で表現できるというのは、かなり美しいというか、数学の便利なところが良く表れています。

回転

最後に回転についてみていきます。

回転はrotate関数で適用することができます。もちろんこの関数も行列(applyMatrix)で表現することができます。

まずはこの関数がどのような行列になるのかを見て、その後行列の合成を計算します。

合成の応用として、図形をその場で回転させる変換をご紹介します。

rotate関数

rotate関数は任意の角度だけ原点(描画領域の左上)中心に座標を回転させる関数です。

原点中心の回転だということに注意が必要です。例えば、

    rotate(HALF_PI/2);//45度回転
    rect(150,50,50,50);

このコードはぱっと見ると四角形をその場で回転させるかのようですが、原点中心回転のため、次のように位置が変わります。

f:id:s-uotani-zetakansu:20181206104407p:plain — 黒：元の位置、赤：rotate後

そのため、rotateを使うときは、次のように中心を原点に合わせて図形を描画し、rotateとtranslateを併用することが多いです。後ほど、その場で図形を回転させる方法(行列)もご紹介します。

translate(100,100);
rotate(HALF_PI/2);
rect(-50,-50,100,100);

この例では45度回転させた後にx,y方向について100ずつずらしています。

もちろん、行列の非可換性から、「rotateの後にtranslateを書いた場合」と「translateの後にrotateを書いた場合」とでは結果が異なります。「適用させたい順と逆順にコードを書く」が基本です。

それでは、rotate関数を行列で表現してみましょう。

回転を表す行列は三角関数を用いて次の形で表現されます。

$$ \begin{pmatrix} \cos t & -\sin t & 0\\ \sin t & \cos t & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

tは角度で、単位はラジアンです。通常の座標平面であれば反時計回りに角度は大きくなっていきますが、Processingでは角度は時計回りに進みます。

回転行列を $R(t)$ と表しておきます。 $(t)$ がついているのは、角度tによって行列の中身が変わるからです。tの関数などと難しいことは考えず、角度tを一つ選ぶと $R(t)$ という行列が一つ決定すると思ってください。

$R(t)$ をベクトル $x$ に作用させてみます。

$$ R(t)x = \begin{pmatrix} \cos t & -\sin t & 0\\ \sin t & \cos t & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\y\\1 \end{pmatrix} = \begin{pmatrix} x\cos t - y\sin t\\ x\sin t + y\cos t \\ 1 \end{pmatrix} $$

新しくできたベクトルを描画して、ちゃんと回転できていることを確かめましょう。

    rect(150,50,50,50);
    stroke("red");
    let x = 150 * cos(HALF_PI/2) - 50 * sin(HALF_PI/2);
    let y = 150 * sin(HALF_PI/2) + 50 * cos(HALF_PI/2);
    rect(x,y,50,50);

f:id:s-uotani-zetakansu:20181206105406p:plain — 黒：元の位置、赤：rotate後

rotate関数は座標全体を回転させるのに対して、上記のコードでは中心座標にしか行列を作用させていないので、表示される場所は同じですが傾いてはいません。

四角形の四隅を回転させて、quad関数で表示させると全く同じになります。

回転行列 $R(t)$ も、もちろん積の順番を入れ替えても同じ行列になります。

$$ R(t)R(s) = R(s)R(t)= R(s+t) $$

t回転してs回転するのと、s回転してからt回転するのとでは結果は確かに同じになりそうです。

同じ角度で何回回転してもこの法則は成り立ちます。

$$ R(t)R(t)R(t) = R(3t)\\ $$ $$ R(t) \ldots R(t) = R(t)^n = R(nt) $$

最後の式は行列の形で書くとよりその凄さが分かります。

$$ \begin{pmatrix} \cos t & -\sin t & 0\\ \sin t & \cos t & 0\\ 0 & 0 & 1 \end{pmatrix}^n = \begin{pmatrix} \cos nt & -\sin nt & 0\\ \sin nt & \cos nt & 0\\ 0 & 0 & 1 \end{pmatrix} $$

それで、回転行列 $R(t)$ と同等なapplyMatrixは次のようになります。

translate(100,100);
applyMatrix(cos(t), sin(t), -sin(t),cos(t),0,0);
rect(-50,-50,100,100);

四角形を描くときに、中心が $(0,0)$ になるように調整していますが、これはrectMode(CENTER)を使うと、もっと簡単に書けます。

rectMode(CENTER);
translate(100,100);
applyMatrix(cos(t), sin(t), -sin(t),cos(t),0,0);
rect(0,0,100,100);

その場で回転させたいんだ！

けどやっぱり回転させるのに、原点に図形を置かないといけないし、translateとrotateの順番を気にしながら書くのはめんどくさい。

そこで、本記事の最後に、rotateとtranslateを組み合わせて、任意の点を中心に座標を回転させる方法をご紹介します。

まずは、登場人物を紹介します。回転の中心 $O: (u,v)$ ,図形の中心 $X:(x,y)$ ,回転角度 $t$ です。

今、回転の中心と図形の中心は下図のような配置になっています。

f:id:s-uotani-zetakansu:20181206110616p:plain

rotateを使って回転させるには、まず $O$ が原点に来るように座標を移動させればいいのです。

translate(-u, -v);

f:id:s-uotani-zetakansu:20181206110749p:plain

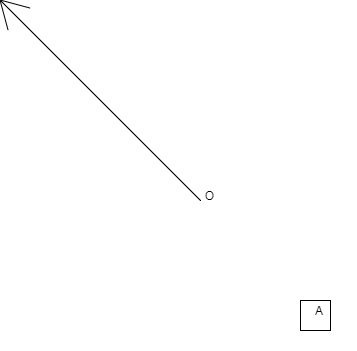
そうしたら、移動後の座標では、 $O$ が座標の中心に移動したので、この状態でrotateを使うと、 $O$ を中心に回転してくれます。

rotate(t);
translate(-u, -v);

f:id:s-uotani-zetakansu:20181206111404p:plain

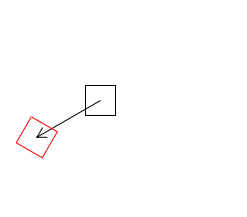
この状態ではまだ $O$ は移動したままなので再びtranslateを使って座標を戻してあげます。

translate(u, v);
rotate(t);
translate(-u, -v);

移動をすべて図に書くと次のようになります。

f:id:s-uotani-zetakansu:20181206112826p:plain

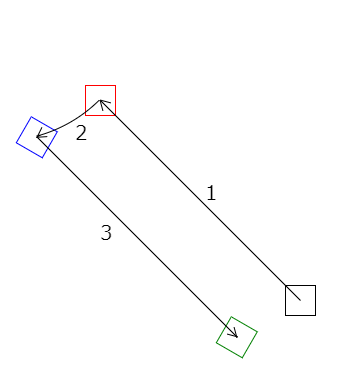
最初の四角形(黒)と最後の四角形（緑）を見比べてみると、ちゃんと、点 $O$ を中心に回転しているようです。

最後に、関数化して名前を付けてあげましょう。

function rotateAt(u,v,t){
  translate(u, v);
  rotate(t);
  translate(-u, -v);
}

この関数を使うと、

rectMode(CENTER);

//その場で回転
rotateAt(100, 100, HALF_PI);
rect(100,100,50,50);

//ある点の周りをぐるぐる
rotateAt(150, 150, frameCount * 0.01);
rect(100,100,50,50);

のように書くことができます。

複雑ですが、この三つの作用も行列の合成で一つにまとめることができます。

$$ \begin{pmatrix} 1 & 0 & u\\ 0 & 1 & v\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos t & -\sin t & 0\\ \sin t & \cos t & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -u\\ 0 & 1 & -v\\ 0 & 0 & 1 \end{pmatrix}\\ = \begin{pmatrix} \cos t & -\sin t & -u\cos t + v\sin t + u\\ \sin t & \cos t & -u\sin t -v\cos t + v\\ 0 & 0 & 1 \end{pmatrix} $$ ここから、applyMatrixを作ると次のようになります。

appyMatrix(cos(t), sin(t), -sin(t), cos(t), -u*cos(t) + v*sin(t) + u, -u*sin(t) -v * cos(t) + v);

この実装を見る限り、できるからと言って無理にapplyMatrixを使うのは得策ではないようです。計算間違いもありえますし

まとめ

いろいろ書きましたが、重要な点をまとめておきます。

scale,translate,rotateはapplyMatrix一つで表現可能
scaleやtranslateは書く順番が異なると結果が異なる
scale,translateなどは、あとから書いたものから順に適用される。これは、この順番に行列の積になっていると覚える
$R(t)^n = R(nt)$
任意の点( $O$ )中心の回転をするには、 $O$ を原点に移し、回転し、 $O$ を元の位置に戻す

最後に

長くなりましたが、最後までお付き合いいただきありがとうございました！

当初は3次元の回転行列を計算して終わろうかと思っていたのですが、さすがに詰め込みすぎだと思い諦めました。

お詫びに、本記事の挿入画像作成に使用した「矢印を描く関数」のコードを残しておきます。(笑)

冒頭に書きました、「Processingはベクトルで支配されている」これは本当だと思います。どこかで行き詰った時には、ベクトル・行列の目線で考えてみるのもいいのではないでしょうか。

おまけ

矢印を描く関数arrowです。引数は、始点(x,y)と終点(x,y)と矢じりの長さです。

function arrow(fromX, fromY, toX, toY, len = 30){
    let d = dist(fromX, fromY,toX,toY);
    if(d===0){return false;}
    let toVect = [len * (fromX - toX)/d, len * (fromY - toY)/d];
    push();
    translate(toX, toY);
    rotate(PI/6);
    line(0,0,toVect[0], toVect[1]);
    pop();
    push();
    translate(toX, toY);
    rotate(-PI/6);
    line(0,0,toVect[0], toVect[1]);
    pop();
    line(fromX, fromY, toX, toY);
}

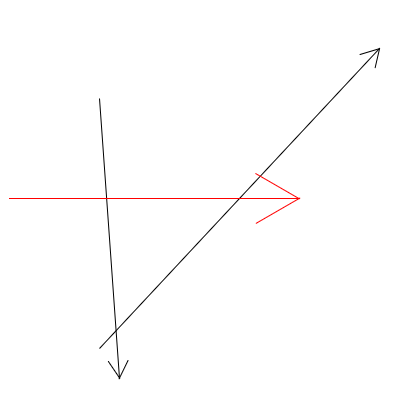
arrow(100,100,120,380,20);
arrow(100,350,120,50,20);
stroke("red");
arrow(10,200,300,200,50);

arrow関数のサンプル

私が運営しているProcessing(p5.js)の入門サイトもよろしくお願いします。

https://processing-fan.firebaseapp.com/

webエンジニアの日常

RubyやPython, JSなど、IT関連の記事を書いています

【p5.js】transformを正しく理解するためのベクトル・行列講座