こんにちは、エンジニアのさもです。

これからTensorFlow関係の記事で何回かmatplotlibを使っていきそうなので、さらっと使い方をおさらいしておきます。

本記事ではjupyter notebookを使うことを想定していますが、%matplotlib inlineを使うことを除けば、同じコードで動きます。

１つの折れ線グラフを表示

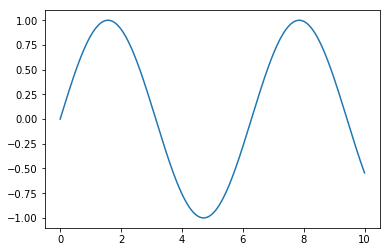
折れ線を表示するだけなら、2本(x軸と対応するy軸)の配列を用意して、plot関数を使えばいいです。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.linspace(0,10,1000)
y = np.sin(x)
plt.plot(x,y)

実行すると以下のようにグラフが表示されます

f:id:s-uotani-zetakansu:20170928130358p:plain

散布図

scatter関数で書くことが出来ます

from numpy.random import randn
x = randn(100)
y = randn(100)
plt.scatter(x,y)

f:id:s-uotani-zetakansu:20170928130656p:plain

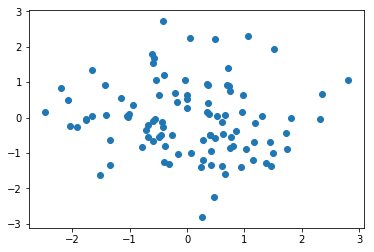
randn関数は、標準正規分布に従って、引数サイズのランダムな値を持つ配列を作ります。

また、scatter関数は引数に点の表示を指定することが出来ます。

2つのグラフを重ねて表示する場合も、特に指定するものは無く、scatterをもう一度書けばいいです。

from numpy.random import randn
x = randn(100)
y = randn(100)
plt.scatter(x,y, marker="x")
x = randn(100)
y = randn(100)
plt.scatter(x,y, marker="*")

f:id:s-uotani-zetakansu:20170928131125p:plain

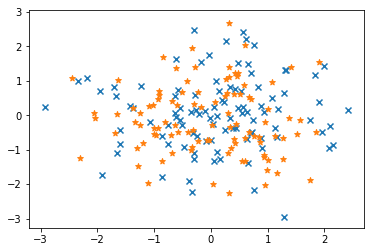
折れ線グラフも同じく、二度plotを書けばグラフを重ねて書くことが出来ます。

複数グラフを表示する

そうではなくて、2つのグラフを重ねずに、別々のグラフとして表示したい場合は、subplotを使います。

ためしに、物体を自由落下させたときの速度と位置のグラフを書いてみましょう。

$t$ は時刻

$h_{0}$ は初期位置。100メートル上から落とす

$v_{0}$ は初速度。上に向かって秒速25メートルで投げる

$g$ は重力定数。重力は下向きに働くので、負の値にしている

時刻 $t$ のときの速度 $v$ は、 $v_{0} + gt$

位置 $h$ は $h_{0} + v_{0}t + \frac{1}{2}gt^{2}$

となります。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

t = np.linspace(0,10,1000)
h0 = 100
v0 = 25
g = -9.8
v = v0 + g * t
h = h0 + v0 * t + g / 2 * t ** 2
# 地面に衝突してから(hが負の値になったら)は高さを0にしている
h = np.clip(h, 0, 1000)
# 地面に衝突してからの速度は0にしている（スライムみたいに、べちゃっと地面にくっつく）
v[np.where(h==0)] = 0

# matplotlibの記述ここから
fig = plt.figure()
subplot_v = fig.add_subplot(2,1,1)
subplot_h = fig.add_subplot(2,1,2)
subplot_v.plot(t, v)
subplot_h.plot(t, h)

上記を実行すると、以下のようになります。

f:id:s-uotani-zetakansu:20170928132404p:plain

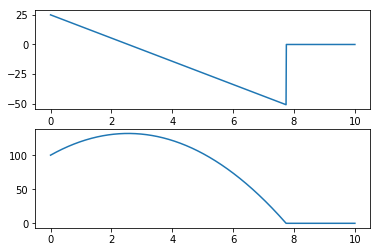
add_subplot(2,1,1)について少し補足です。

add_subplotは表示位置を指定することが出来ます。

引数の1つ目が、行数、2つ目が列数、そして、3つ目がその何番目に表示するかを指定します。

上記コードを

subplot_v = fig.add_subplot(1,2,1)
subplot_h = fig.add_subplot(1,2,2)

に変えると、1行2列になるように並びます。

並び順は、左上から配置していき、右へ進みます。

右端まできたら、一つ下の行の一番左へ移動します。

最後に

一番よく使うであろう折れ線グラフと、散布図の表示を復習してみました。

今まで私が使ったグラフ表示プログラムの中で、一番簡単で直感的だと思います。

自由落下を書いていてふと思いついたのですが、「時速○キロのトラックにぶつかるのは、ビル△階から落下するのと同じ衝撃」っていうのを昔よく見ましたよね。

ちょっと計算してみたいと思います。

# トラックの速度（km/h）
v = 40
# 単位の変換(km/h  ->  m/s)
s = v * 1000 / 3600
# 重力加速度9.8で加速していって、秒速sメートルに達するまでの時間
t = s / 9.8
# 重力加速度9.8で加速していって、t秒後の移動距離
h = 4.9 * t ** 2
# ビル何階に相当するか（1階を3.5メートルで換算）
# 例えば、ビル3階部分から落ちたときは、２階の高さから落ちることになるので、+1している
rank = h / 3.5 + 1